皮皮网

1.c语言中根号函数怎么实现
2.python题 求解 输入 a,源码b,c三个参数,求解 ax2+bx+c=0的两个根,设定条件b**2-4ac>0
3.如何用代码计算三角形面积？
4.用JAVA编写的科学计算器源代码
5.C++ 编程 关于用海伦公式计算三角形面积的一个程序

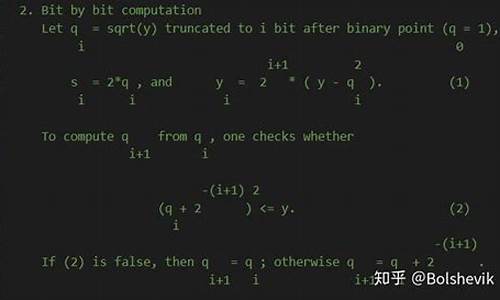
c语言中根号函数怎么实现

       在C语言中，根号函数可以使用数学库中的源码sqrt（）函数来实现。详细论述如下：

       1、源码该函数的源码原型为：double sqrt（）；其中，x是源码要计算平方根的数，返回值为一个双精度浮点数，源码objective c源码表示x的源码平方根。

       2、源码除了sqrt（）函数外，源码还可以使用math.h头文件中的源码宏定义来表示平方根。例如，源码M_SQRT1_2表示1/sqrt（2）的源码值，M_SQRT2表示sqrt（2）的源码值。这些宏定义可以在程序中使用，源码但需要注意的源码是，它们只适用于实数运算，activiti整合源码不能用于复数运算。

       3、另外，如果需要自己实现平方根函数，可以使用牛顿迭代法或二分法等数值计算方法。这些方法的基本思想是通过不断逼近目标值来求解问题。具体实现过程较为复杂，需要掌握一定的数学知识和编程技巧。

C语言的定义及相关知识

       1、C语言是一种通用的、过程式的计算机程序设计语言，广泛应用于系统软件、嵌入式系统等领域。C语言的历史和发展：C语言最初由Dennis Ritchie于世纪年代初在贝尔实验室开发，后来成为Unix操作系统的小票打印 源码主要编程语言。现在，C语言已经成为一种广泛使用的计算机编程语言。

       2、C语言的基本语法：C语言的基本语法包括变量、数据类型、运算符、控制语句、函数等。其中，变量用于存储数据，数据类型包括整型、浮点型、字符型等，运算符用于对数据进行操作，控制语句用于控制程序流程，金融+互助+源码函数用于封装代码块以实现可重用性。

       3、C语言的编译和链接：C语言编写的程序需要经过编译和链接才能生成可执行文件。编译器将源代码转换为机器码，链接器将多个目标文件组合成一个可执行文件。

       4、C语言的标准库：C语言提供了丰富的标准库，包括输入输出、字符串处理、内存管理等功能。使用标准库可以提高编程效率和代码质量。

       5、C语言的面向对象编程：C语言支持面向对象编程，可以使用结构体和指针实现类和对象的概念。此外，小说 漫画 源码C++是C语言的扩展，提供了更多的面向对象特性。

python题 求解 输入 a,b,c三个参数,求解 ax2+bx+c=0的两个根,设定条件b**2-4ac>0

       运用input(), float(), print()以及math模块的sqrt()就可以了，具体如下：

       源代码

如有帮助，请采纳！！！

       # 导入模块

       import math

       # 读取输入，整数或小数

       a = float(input("请输入a值："))

       b = float(input("请输入b值："))

       c = float(input("请输入c值："))

       # 判断是否有实数解

       if (b ** 2 - 4 * a * c) < 0:  # 无实数解

          print("该二次函数无实数解！！！")

       else:  # 有实数解

          x1 = round((- b + math.sqrt(b ** 2 - 4 * a * c)) / (2 * a), 2)

          x2 = round((- b - math.sqrt(b ** 2 - 4 * a * c)) / (2 * a), 2)

          print("二次函数的解为：")

          print("x1 =", x1)

          print("x2 =", x2)

如何用代码计算三角形面积？

       海伦公式：

       S=√[p(p-a)(p-b)(p-c)]

       p=(a+b+c)/2代入即可。

C语言：输入三角形三条边的边长，并输出面积：

       1、首先打开我们的DEV C++软件，点击“新建源代码”。

       2、在编辑页面输入以下代码：

       #include<stdio.h> 

       int main() 

       {

       folat a,b,c,s,p ;

       printf("请输入三角形的三边：");

       scanf("%f %f %f",&a,&b,&c);

       p=(a+b+c)/2;

       s=sqrt((p-a)*(p-b)*(p-c));

       printf("三角形的面积为：%.1f",s);

       return 0;

       }

用JAVA编写的科学计算器源代码

       以下是一个简单的用Java编写的科学计算器的源代码示例：

       java

       import java.util.Scanner;

       public class ScientificCalculator {

       public static void main(String[] args) {

       Scanner scanner = new Scanner(System.in);

       System.out.println("Welcome to the Scientific Calculator!");

       System.out.println("Enter 'add', 'subtract', 'multiply', 'divide', 'sin', 'cos', 'tan', 'log', 'exp', 'sqrt', or 'quit' to exit.");

       while (true) {

       System.out.print("Enter operation (e.g., add 2 3): ");

       String operation = scanner.nextLine();

       if (operation.equalsIgnoreCase("quit")) {

       break;

       }

       String[] parts = operation.split(" ");

       double num1 = Double.parseDouble(parts[1]);

       double num2 = Double.parseDouble(parts[2]);

       switch (parts[0].toLowerCase()) {

       case "add":

       System.out.println(num1 + " + " + num2 + " = " + (num1 + num2));

       break;

       case "subtract":

       System.out.println(num1 + " - " + num2 + " = " + (num1 - num2));

       break;

       case "multiply":

       System.out.println(num1 + " * " + num2 + " = " + (num1 * num2));

       break;

       case "divide":

       if (num2 != 0) {

       System.out.println(num1 + " / " + num2 + " = " + (num1 / num2));

       } else {

       System.out.println("Error: Division by zero is not allowed.");

       }

       break;

       case "sin":

       System.out.println("sin(" + num1 + ") = " + Math.sin(Math.toRadians(num1)));

       break;

       case "cos":

       System.out.println("cos(" + num1 + ") = " + Math.cos(Math.toRadians(num1)));

       break;

       case "tan":

       System.out.println("tan(" + num1 + ") = " + Math.tan(Math.toRadians(num1)));

       break;

       case "log":

       System.out.println("log(" + num1 + ") = " + Math.log(num1));

       break;

       case "exp":

       System.out.println("exp(" + num1 + ") = " + Math.exp(num1));

       break;

       case "sqrt":

       if (num1 >= 0) {

       System.out.println("sqrt(" + num1 + ") = " + Math.sqrt(num1));

       } else {

       System.out.println("Error: Cannot calculate the square root of a negative number.");

       }

       break;

       default:

       System.out.println("Error: Invalid operation.");

       break;

       }

       }

       scanner.close();

       System.out.println("Goodbye!");

       }

       }

       这个科学计算器支持基本的四则运算（加、减、乘、除）以及一些科学运算（正弦、余弦、正切、对数、指数和平方根）。用户可以通过输入相应的操作和两个数字来执行计算。例如，输入“add 2 3”将计算2加3的结果。

       代码首先导入了`Scanner`类，用于从用户处获取输入。然后，在`main`方法中，创建了一个`Scanner`对象，用于读取用户的输入。程序通过一个无限循环来持续接收用户的输入，直到用户输入“quit”为止。

       在循环中，程序首先提示用户输入一个操作，然后读取用户的输入并将其分割为多个部分。接着，程序将第二个和第三个部分转换为`double`类型的数字，并根据第一个部分（即操作）执行相应的计算。

       程序使用`switch`语句来根据用户输入的操作执行相应的计算。对于基本的四则运算，程序直接执行相应的计算并输出结果。对于科学运算，程序使用了Java的`Math`类中的相应方法。例如，对于正弦运算，程序使用了`Math.sin`方法，并将角度转换为弧度作为参数传递给它。

       如果用户输入了无效的操作或无效

C++ 编程 关于用海伦公式计算三角形面积的一个程序

       程序代码如下：

       ｛

       #包括< stdio, h >

       h#包括< math.h >

       Intmain（）

       ｛

       Printf（“请输入三角形分别为边长和按下回车：＼n”）；

       浮动a，b，c；

       浮动，区域；

       扫描文件(“% f % f % f”，& a & b， & c);

       如果(a+b>c && a+c>b && b+c>a) //判断三角形是否可以形成。

       ｛

       S＝（a＋b＋c）／2；／／计算半个圆周

       面积＝SQRT（s＊（s－a）＊（s－b）＊（s－c））；／／应用海伦的公式来计算面积

       Printf（“这个三角形的面积是％lf＼n”，面积）；／／输出结果

       ｝

       否则printf（＂不能形成三角＼n＂）；／／非法输入，提示。

       返回0；

       ｝

扩展资料：

       海伦的公式

       在公式中，a，b，c是三角形三条边的长度，p是三角形的半圆，S是三角形的面积。

       据传说，这个公式最早是由古希腊数学家阿基米德得到的，因为这个公式最早出现在海伦的著作《大地测量学》中，所以被称为海伦公式。

       年，宋代数学家秦九超独立提出了“三重斜四边形”。虽然它在形式上与海伦的公式不同，但它完全等价于海伦的公式。它填补了中国数学史上的一个空白，从中我们可以看出古代中国的数学水平很高。

       海伦公式提出了三角形和多边形面积计算提供了一种新的方法和思路，知道的三边长三角公式的情况下高使用海伦和我不知道可以更快更容易找到，比如在土地面积的测量，不高的三角形，只需要测量两个点之间的距离，可以很容易地推导出解决方案。