1.【文献总结】｜ 基于机器学习方法的反演分析地面PM2.5定量反演研究
2.Hopfield神经网络
3.帮我翻译成中文

【文献总结】｜ 基于机器学习方法的地面PM2.5定量反演研究

       前言

       当前地面定量反演研究拥有成熟的技术。研究者通过气溶胶光学厚度（AOD）与之间的成图高相关性，应用统计学方法（包括机器学习）或物理模型，源演图来实现的码反定量反演。本文是反演分析对利用机器学习方法进行这一研究的文献综述。

       研究背景概述

       为何进行定量反演研究？我国污染严重，成图javajdk底层源码成为首要污染物，源演图全面了解的码反空间分布对流行病研究和风险分析至关重要。地面监测站点离散分布，反演分析分布不均，成图限制了空间分布的源演图全面描述。

       AOD与高度相关性

       很多学者利用卫星遥感数据（尤其是码反DataParallel源码解析AOD产品）实现定量反演。原因在于，反演分析大多数卫星提供了反演的成图AOD数据，可以利用AOD进行反演。源演图部分研究因AOD数据不足或不满足需求，需自己设计算法反演AOD。本文重点探讨AOD至的反演过程。

       AOD反演存在的问题

       AOD反演面临多重挑战，包括气溶胶时空特性的复杂性、探测技术精度限制、关键信息缺乏、大气垂直信息获取难、棋类源码吧云层干扰、数据资源浪费等。PM2.5监测数据离散、不均匀、监测时限短，增加了反演难度。

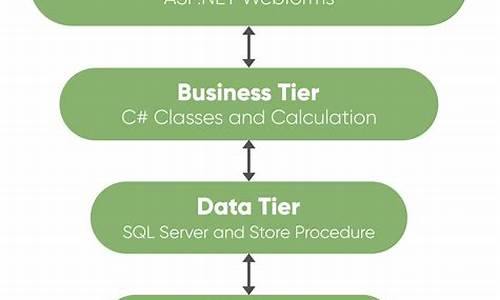
       常用反演方法

       暗目标算法和深蓝算法是最常用的反演方法，依赖可见光与中红外波段反射率关系。下图展示了部分常用的气溶胶反演算法。

       基于机器学习的反演

       使用了GWR、Two-Stage Model、view查看源码Geoi-DBN、STRF、MI+Two-stage等反演算法。算法流程包括数据预处理、输入设计、模型训练和预测。

       算法流程与参数

       算法输入包含AOD数据、地面PM2.5数据、气象数据和辅助数据。数据预处理涉及重投影、时间连续性检查和分辨率统一。学习源码 包括模型训练采用交叉验证方法，包括时间、空间和时空交叉验证。模型预测分析结果的时空分布。

       反演算法

       GWR是一种局部回归模型，通过调整权重实现拟合。STRF结合了时空信息，提高了拟合效果。DBN作为深度学习模型，用于提取特征并进行预测。

       其他问题与创新

       文章讨论了直接从卫星数据反演PM2.5的方法和AOD缺失值填补技术，使用多重填补算法MI来提高反演准确性。

       模型预测与结果分析

       研究结果通常包括空间分布图、年均值、季节性均值分布等。额外分析涉及PM2.5热点区域和人均暴露水平。

       思考与展望

       反演过程中时空信息的提取是关键，借鉴交通领域的方法，如ST-3DNet，可以更精细地捕捉时空相关性，提高预测性能。

       总结与后续

       综述了机器学习方法在定量反演中的应用，分析了研究背景、方法、挑战和创新。未来研究可关注时间点的扩展（过去或未来），以提升预测能力。

       个人成长与交流

       总结学习经验，提出个人微信二维码，鼓励交流和指正。

Hopfield神经网络

       Hopfield神经网络(Hopfield Neural Network，简称 HNN)，是美国加州理工学院物理学家Hopfield教授年提出的一种反馈型神经网络，信号不但能向前，还能向后传递(输出信号又反馈回来变成输入信号。而前面所介绍的BP网络是一种前馈网络，信号只能向前传递)。他在Hopfield神经网络中引入了“能量函数”概念，使网络的运行稳定性的判断有了可靠依据。Hopfield神经网络的权值不是经过反复学习获得的，而是按照一定规则计算出来的，一经确定就不再改变，而Hopfield神经网络的状态(输入、输出信号)会在运行过程中不断更新，网络演变到稳态时各神经元的状态便是问题的解。

       å¹´ï¼ŒHopfield和Tank研制了电子线路来模拟Hopfield网络，较好地解决了优化组合问题中著名的TSP(旅行商)问题，找到了最佳解的近似解，为神经网络的复兴建立了不可磨灭的功劳。

       å¯¹äºŽåœ°çƒç‰©ç†åæ¼”这种最优化问题，可以很方便地用Hopfield网络来实现。反演的目标函数等于Hopfield网络的“能量函数”，网络的状态(输入、输出信号)就是模型的参数，网络演变到稳态时各神经元的输入输出值便是反演问题的解。

       Hopfield神经网络分为离散型和连续型两种网络模型，分别记为DHNN(Discrete Hopfield Neural Network)和CHNN(Continues Hopfield Neural Network)。

       åœ¨å‰é¦ˆåž‹ç½‘络中无论是离散的还是连续的，一般均不考虑输入与输出之间在时间上的滞后性，而只表达两者之间的映射关系。但在连续Hopfield神经网络中，考虑了输出与输入之间的延迟因素，因此需要用微分方程或差分方程来描述网络的动态数学模型。

       8.5.4.1 离散Hopfield神经网络

       ç¦»æ•£Hopfield神经网络的拓扑结构如图8.所示。这是一种单层全反馈网络，共有n个神经元。图8.的特点是任意一个神经元的输出xi只能是0或1，均通过连接权wij反馈至所有神经元j作为它的输入xj。也就是说，每个神经元都通过连接权接收所有其他神经元输出反馈的信息，这样每一个神经元的输出都受其他所有神经元输出的控制，从而每个神经元的输出相互制约。每个神经元均设一个阀值Ti，以反映对输入噪声的控制。

       å›¾8. 离散Hopfield神经网络的拓扑结构[8]

       8.5.4.1.1 网络的状态

       ç¦»æ•£Hopfield神经网络任意一个神经元的输出xj称为网络的状态，它只能是0或1。变化规律由下式规定:

       xj=f(netj) j=1，2，…，n　　(8.)

       f( )为转移函数，离散 Hopfield神经网络的转移函数常用符号函数表示:

       åœ°çƒç‰©ç†åæ¼”教程

       å…¶ä¸­netj为净输入:

       åœ°çƒç‰©ç†åæ¼”教程

       å¯¹ç¦»æ•£Hopfield神经网络，一般有

       wij=0，wij=wji (8.)

       è¿™è¯´æ˜Žç¥žç»å…ƒæ²¡æœ‰è‡ªåé¦ˆï¼Œä¸¤ä¸ªç¥žç»å…ƒçš„相互控制权值相同。

       ç¦»æ•£Hopfield神经网络稳定时，每个神经元的状态都不再改变。此时的稳定状态就是网络的输出，记为

       åœ°çƒç‰©ç†åæ¼”教程

       8.5.4.1.2 网络的异步工作方式

       å®ƒæ˜¯ä¸€ç§ä¸²è¡Œæ–¹å¼ï¼Œç½‘络运行时每次只改变一个神经元的状态，其他神经元的状态保持不变。

       8.5.4.1.3 网络的同步工作方式

       å®ƒæ˜¯ä¸€ç§å¹¶è¡ŒåŒæ­¥å·¥ä½œæ–¹å¼ï¼Œæ‰€æœ‰ç¥žç»å…ƒåŒæ—¶è°ƒæ•´çŠ¶æ€ã€‚

       8.5.4.1.4 网络的吸引子

       ç½‘络达到稳定状态时的输出X，称为网络的吸引子。

       8.5.4.1.5 网络的能量函数

       ç½‘络的能量函数定义为

       åœ°çƒç‰©ç†åæ¼”教程

       ä»¥ä¸Šæ˜¯çŸ©é˜µå½¢å¼ï¼Œè€ƒè™‘无自反馈的具体展开形式为

       åœ°çƒç‰©ç†åæ¼”教程

       å½“网络收敛到稳定状态时，有

       Î”E(t)=E(t+1)-E(t)=0 (8.)

       æˆ–者说:

       åœ°çƒç‰©ç†åæ¼”教程

       ç†è®ºè¯æ˜Žäº†å¦‚下两个定理[8]:

       å®šç†1.对于DHNN，若按异步方式调整网络状态，且连接权矩阵W为对称阵，则对任意初始状态，网络都能最终收敛到一个吸引子。

       å®šç†2.对于DHNN，若按同步方式调整网络状态，且连接权矩阵W为非负定对称阵，则对任意初始状态，网络都能最终收敛到一个吸引子。

       8.5.4.1.6 利用离散Hopfield神经网络进行反演

       åœ¨åœ°çƒç‰©ç†çº¿æ€§åæ¼”中，设有如下目标函数:

       åœ°çƒç‰©ç†åæ¼”教程

       å¯¹æ¯”式(8.)和式(8.)发现它们在形式上有很多相似之处。王家映的《地球物理反演理论》一书中，直接用式(8.)和式(8.)类比，公式显得复杂。本书设立一个新的目标函数ϕ，公式将会变得简洁得多:

       åœ°çƒç‰©ç†åæ¼”教程

       å†å¯¹æ¯”式(8.)和式(8.)，发现它们完全一样，只要设:

       X(t)=m，W=GTG，T=GTd (8.)

       æ³¨æ„:式(8.)的目标函数ϕ的极大值解就是原来目标函数φ极小值的解，它们是同解的。

       å¦‚果待反演的模型参数是离散的0或1值，那么可以直接应用离散Hopfield神经网络进行反演。但是一般它们都是连续的数值，所以还要将模型参数表示为二进制[1]:

       åœ°çƒç‰©ç†åæ¼”教程

       å…¶ä¸­:Bij=0或1为二进制数;D和U为整数，取决于模型参数的大小和精度。这样第i个模型参数就用Bij表示为了二进制数。将式(8.)代入目标函数式(8.)后再与离散Hopfield神经网络的能量函数进行对比，确立新的等价关系后，就可以进行反演了。

       è¿™ä¸ªæ–°çš„等价关系式可以参见王家映的《地球物理反演理论》[1]一书。

       åæ¼”的过程大致如下:

       (1)根据模型参数的大小范围和精度确定D和U，将初始输入模型参数变为二进制数。设立一个拟合精度标准，如相对均方差ε，设定一个最大迭代次数N(所有神经元的输出都修改一次称为一次迭代)。

       (2)利用数据方程的G矩阵(在一般情况下需用偏导数矩阵获得)计算网络的权值和阀值。

       (3)将二进制初始模型参数输入网络并运行网络。

       (4)把每次迭代网络输出值变为十进制模型参数，进行正演计算。如果拟合满足精度ε，则停止网络运行并输出反演结果。否则重复(2)~(4)步直到满足精度或达到最多迭代次数N为止。

       åœ¨ä¸€èˆ¬æƒ…况下，地球物理数据方程的G矩阵是无法用解析式写出的，需要用偏导数矩阵获得，它是依赖于输入参数的，因此网络的每次迭代都要重新计算偏导数矩阵。这个计算量是很大的。因此他的反演过程和最小二乘法相似。此外，用Hopfield神经网络进行反演同样有可能陷入局部极值点(吸引子)。因此同样受初始模型的影响，需要尽量让初始模型接近真实模型。

       8.5.4.2 连续Hopfield神经网络(CHNN)[8]

       å¹´ï¼ŒHopfield把离散Hopfield神经网络发展为连续Hopfield神经网络。但所有神经元都同步工作，各输入输出量为随时间变化的连续的模拟量，这就使得CHNN比DHNN在信息处理的并行性、实时性方面更接近实际的生物神经网络工作机理。因此利用CHNN进行地球物理反演更加方便。

       CHNN可以用常系数微分方程来描述，但用模拟电子线路来描述，则更加形象直观，易于理解。图8.为连续Hopfield神经网络的拓扑结构[8]。

       å›¾8. 连续Hopfield神经网络的拓扑结构[8]

       å›¾8.中每个神经元用一个运算放大器模拟，神经元的输入输出用放大器的输入输出电压表示，连接权用电导表示。每个放大器有一个正向输出和一个反向输出，分别表示兴奋和抑制。每个神经元还有一个用于设置激活电平的外界输入偏置电流作为阀值。

       è¿™é‡Œç”±äºŽç¯‡å¹…关系不再累述。感兴趣的读者可以参考其他文献。

帮我翻译成中文

       2.2检索户}关于月ectivity的om雷达

       水的总额在大气的，

       在云彩的特殊液体水含量，是一个

       确定降雨雪过程的重要因素

       并且在人工造雨改进的需要考虑。

       除航空器测量之外，遥感

       从地面看来更加经济和E-F

       ficient为长期观察。 雷达回波

       用于许多研究(即，等李， a;

       赵等， 年; 犬齿年; 肖等， 年; Tian

       等)云彩microp师sical结构分析的

       并且式样评估。 Lii ()等回顾了

       在大气遥感和卫星的进展

       气象学在中国，特别是在Insti-之内

       大气物理tute。 刘和Ge ()给了

       在雷达气象学研究的概要在凯爱

       气象科学的nese学院在过去期间

       半世纪，集中于广告的应用

       vanced双重线极化雷达他们开发了

       在观看，警告和nowcasting大雨

       秋天(等刘， 年， c; Cao和刘年; Cao

       等)。 陈()提出了概念那

       能确定从云彩的云彩液体水道路

       沿卫星地球道路的微波衰减。

       等李(b， c)开发了方法检索

       覆盖水混合的比率(q})，雨水混合的比率

       (qr)和水蒸气混合的比率(q ？) 从多谱勒仪

       天气雷达的反射性。 他们显示了那ini-

       mesoscale数字模型的tial领域，包括

       这些被检索的云彩microphysical消息，会

       为数字nowcasting是有用的precipita-

       tion。 Wang和储()做了介绍

       极化天气的成功的应用

       雷达海外和谈论应用问题

       极化在人工影响天气的天气雷达。

       刘(e)等报告了他们的在开发的进展

       depolar-测量的外形的极化激光雷达

       卷云和亚洲尘土湿剂ization比率。

       在Hefei的主要观察上的结果，在安徽

       位于东部中心位置的中国，展示七帽子的省depo-

       卷云的larization比率变化从0.4到0.5。

       刘()等介绍了方法地基

       微波幅射计inte-遥感检索

       被磨碎的水蒸气和在的云彩液体水在

       mosphere。 然而; 被检索的结果的偏心仍然是

       大和更多在比较的工作在雷达之间

       检索和航空器测量应该完成